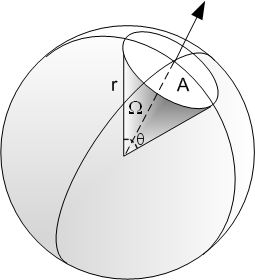
|
A solid angle is similar in 3 dimensions to a plane angle in 2 dimensions.
A solid angle Ω is equal to the ratio of the viewed surface A divided by the square of the viewed distance r.
Ω=A/r^2
It is expressed in steradian (sr), the official SI unit - international system of units. It is comprised of numbers between 0 and 4π sr for a whole sphere.
For a regular cones, solid angle Ω is equal to Ω =2 π x (1 - cos(θ/2))
where θ is the plane angle of a cone apex. For example, a hemisphère (half ball) has a plan angle θ of π rd and a solid angle of 2π sr
If we reverse the previous formula, we can deduct the plane angle θ from the solid angle Ω :
θ = 2 x arccos(1- Ω/2π)
For example, the apparent diameter of the moon seen from earth is θ=0.5 °, which is equivalent to a solid angle of about 6e-5 steradian.
Reading eyes vision field is θ=3 ° (0.002 sr) (foveal zone).
The peripheral vision field of eyes is about θ=25 ° (ellipse shape with -15° left, +15 ° right, -8° high, +12° low) so about 0.15 sr.
The following field is a solid angle Ω of a regular cone whose plane angle θ is indicated on the top array.
|
